안녕하세요, 애옭입니다!
오늘은 "단순 조화 운동하는 물리계의 위치 에너지와 운동 에너지"에 대해 알아보겠습니다!
'음향학'을 공부하는 데 있어서, 위치 에너지와 운동 에너지를 이해하는 것은 정말로 중요합니다.
왜냐하면, "음향학"의 연구 대상인 "음파"가 매질의 종방향 운동 에너지와 위치 에너지의 상호적인 전환이 전파되는 것이기 때문입니다.
따라서 음향학을 공부하시는 음향학도 여러분들께, 오늘 설명해 드리는 위치 에너지와 운동 에너지의 개념을 이해하는 것은 정말 중요하다고 백 번 천 번 말씀드리고 싶습니다.
오늘 내용은 조금 길기에, 바로 시작하겠습니다!
* (본 글에서는 '위치 에너지'를 기술할 때, 공식적인 영문 명칭인 '퍼텐셜 에너지(Potential Energy)'를 종종 사용합니다. 간단히 정리하여, '위치 에너지' = '퍼텐셜 에너지'이니 너무 혼동하지는 마셨으면 좋겠습니다.)
우선 단순 조화 운동하는 물리계의 위치 에너지와 운동 에너지를 이야기하기 전에, 먼저 "단순 조화 운동하는 물리계의 유동에 관한 운동 방정식의 초기 조건"을 유도하여야 합니다.
지난 글에서 유도하였던 단순 조화 운동하는 물리계(단진자)의 운동 방정식에서, 일반해 x_1(Sine), x_2(Cosine)를 사용하여, 운동 방정식의 초기 조건을 유도하도록 하겠습니다!
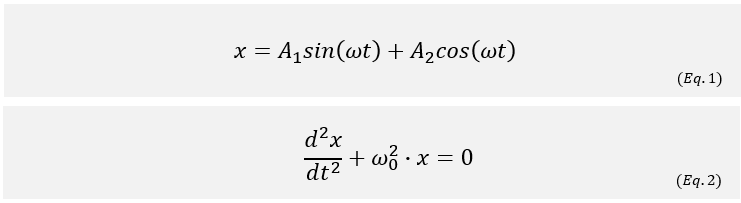
'초기 조건(Initial Condition)'은 '시간' 또는 '공간'의 초기값이 0인 그 시점 자체에서, 운동 방정식의 해가 만족시키는 운동의 조건을 의미합니다.
(Eq. 2)의 초기 조건을 구하기 위하여 시간의 변위가 0인, 즉 t = 0인 시점에서의 운동만을 고려하도록 하겠습니다!

[Eq. 1 → Eq. 3]
일반해 (Eq. 1)에 초기 조건 x = x_0, t = 0을 적용합니다. cos(0) = 1이고, sin(0) = 0임을 이용하여 초기 위치 변위 x_0은 Cosine 항이 포함된 일반해의 진폭 A_2와 같음을 알 수 있습니다.
[Eq. 1 → Eq. 4]
일반해 (Eq. 1)을 시간에 대하여 미분하고, 초기 위상 속도 u = u_0임을 대입하면, 초기 위상 속도는 고유 각 주파수 w와 Cosine 항의 진폭 A_2의 곱과 같음을 알 수 있습니다.
(미분하기 전엔) 우변의 왼쪽 항은 Sine 항이고, 오른쪽 항은 Cosine 항이었습니다!
또는, (Eq. 4)에서 A_1을 A_1 = -Asin(φ), A_2을 A_2 = Acos(φ)로 치환하여 위상과 진폭의 초기 조건을 만족하는 운동 방정식의 일반해 (Eq. 5)를 구할 수도 있습니다.

다시 한 번 정리하자면, (Eq. 5)의 'φ'은 '초기 위상각(Initial Phase Angular)', 'A'는 운동의 '초기 진폭(Initial Amplitude)'입니다!
(Eq. 5)에 초기 조건 x = x_0, t = 0을 대입하여 정리하면, φ과 A는 (Eqs. 6~7)과 같이 정리됩니다.

[Eq. 5 → Eq. 6]
일반해 (Eq. 5)에 초기 조건 x = x_0, t = 0을 적용하고 간단한 수학적 조작을 취하면, 초기 진폭 A는 초기 위치 변위 x_0와 입자 속도, 고유 각 주파수 비의 합으로 (Eq. 6)과 같이 기술됩니다.
[Eq. 5 → Eq. 7]
일반해 (Eq. 5)에 초기 조건 x = x_0, t = 0을 적용하고 간단한 수학적 조작을 취하면, 초기 위상 φ는 입자 속도와 고유 각 주파수, 초기 위치 변위의 비로 (Eq. 7)과 같이 기술됩니다.
'속도(Speed)'는 시간에 따른 거리의 변위, 즉 '위치의 증분(거리의 차이)'를 시간으로 미분한 값입니다.
따라서 (Eq. 5)를 시간에 대하여 미분하면, 물리계의 유동 속도를 (Eq. 8)과 같이 얻을 수 있습니다!

이렇게 위치 에너지와 운동 에너지를 설명하기 위한 운동 방정식의 초기 조건 유도를 모두 마쳤습니다.
이제 정말로 이번 글의 주제인, "위치 에너지"와 "운동 에너지"에 대해서 알아보도록 하겠습니다!
단순 조화 운동하는 임의의 물리계의 '위치 에너지(Potential Energy)'는, 스프링에 연결되어 있는 질량이 정적인 평행 상태에서 벗어나 스프링을 변형시키는 데 사용된 모든 일의 합으로 정의됩니다.
이는 즉 '단순 조화 운동하는 임의의 물리계에서의 위치 에너지'는 '복원력'을 스프링의 운동 방향에 대하여 적분한 값, 즉 (Eqs. 9~10)으로 기술될 수 있음을 의미합니다.

[Eq. 9]
단순 조화 운동하는 물리계의 질량에 대한 퍼텐셜 에너지는 스프링에 대해 행한 일의 모든 합이므로, 이는 복원력의 운동 방향에 대한 적분으로 기술할 수 있습니다. 간단한 적분 공식을 통하여, Integral [sx]dx를 (sx^2 / 2)로 고쳐 기술합니다.
[Eq. 9 → Eq. 10]
(Eq. 9)의 운동 방향 x에, (Eq. 5)에서 구한 초기 위상각과 진폭을 만족하는 운동 방정식의 일반해를 대입합니다. 그 결과로서, 단순 조화 운동하는 물리계의 질량에 대한 퍼텐셜 에너지는 (Eq. 10)으로 최종 정리됩니다.
일반적으로 물리계의 '운동 에너지(Kinetic Energy)'는 질량과 속도의 제곱을 2로 나눈 값이므로, 초기 위상을 만족하는 물리계의 유동 속도 (Eq. 8)을 대입하여 (Eqs. 11~12)로 기술할 수 있습니다.

[Eq. 11]
대부분의 물리계에서 운동 에너지는, 질량과 속도의 제곱의 곱을 2로 나눈 값입니다.
[Eq. 11 → Eq. 12]
(Eq. 11)에서 속도의 제곱(u^2)의 위치에 (Eq. 8)에서 구한 질량의 유동 속도를 직접 대입합니다. 그 결과로서, 단순 조화 운동하는 물리계의 질량에 대한 운동 에너지는 (Eq. 12)로 최종 정리됩니다.
물리계의 '기계적 에너지(Mechanical Energy[역학적 에너지])'는 위치 에너지와 운동 에너지의 합이므로, (Eq. 10)과 (Eq. 12)를 더하여 이 물리계의 기계적 에너지를 유도할 수 있습니다.

[Eq. 13]
기계적 에너지는 물리계의 운동 에너지와 위치 에너지의 합입니다. 운동 에너지 (Eq. 12)와 퍼텐셜 에너지 (Eq. 10)을 더하여 기계적 에너지 (Eq. 13)을 유도합니다.
[Eq. 13 → Eq. 14]
복원력 s가 s = m*ω_0^2이고, 유동 속도 진폭 U이 U = ω_0*A임을 이용하여 (Eq. 13)을 간단히 해 줍니다.
[Eq. 13 → Eq. 15]
또는, 삼각 함수의 합성에 대한 항등식 <sin^2(x)+cos^2(x) ≡ 1>을 이용하여, (Eq. 15)의 꼴로 정리할 수 있습니다.
두 식 (Eq. 14), (Eq. 15)는 기계적 에너지에 대한 수리적 해석의 이원성으로 인해 도출되는 각각의 수식입니다. 따라서, 두 식 중 어느 식을 사용하여도 그 의미는 '기계적 에너지'를 나타내는 것에 반하지 않으며, 단지 상황과 맥락에 맞는 수식을 사용하여 그 편리성을 증진할 수 있을 뿐입니다.
이렇게 "단순 조화 운동하는 물리계의 위치 에너지와 운동 에너지"에 대해 알아보았습니다.
오늘 유도한 두 에너지는 굳이 음향학이 아니더라도 다른 물리학적인 과목에서나, 아니면 공학적인 과목에서도 유용하게 사용되는 지식이니 여러분들이 꼭 알고 넘어가셨으면 하는 부분입니다.
혹시 이해가 안 되시는 부분이나 궁금하신 부분이 있으시다면 언제든지 댓글로 남겨주세요!
확인해 보고, 시간될 때 열심히 답변해 드리도록 하겠습니다.
그럼 오늘 글도 이만 마치겠습니다. 읽어주셔서 감사합니다!
2022. 09. 28
애옭 올림
[Reference]
[1] Lawrence E. Kinsler, “Fundamentals of Acoustics” (in USA), John Wily & Sons Inc. (1999)
[2] D. T. Blackstock, "Fundamental of Physical Acoustics" (in USA), John Wiley & Sons Inc. (2000)
Copyrights ⓒ 애옭 at Hyonmin
'Basic Theory :: 음향학을 위한 기초 이론들 > Basic Physics :: 기초 물리학' 카테고리의 다른 글
| Basic Physics(기초 물리학) :: 선형 파동 방정식 - 종방향 조화 운동 (0) | 2022.11.12 |
|---|---|
| Basic Physics(기초 물리학) :: 선형 파동 방정식 - 횡방향 조화 운동 (1) | 2022.11.06 |
| Basic Physics(기초 물리학) :: 물성표 (0) | 2022.10.10 |
| Basic Physics(기초 물리학) :: 에너지와 일, 열역학 제1법칙 (1) | 2022.10.06 |
| Basic Physics(기초 물리학) :: 단순 조화 운동하는 물리계의 운동 해석 (3) | 2022.09.26 |