안녕하세요, 효온민입니다.
아주 오랜만에 블로그에 들어온 것 같습니다.
이 글은 음향 파동 방정식을 유도하기 위한 두 번째 과정으로, 압축성 유동하는 비점성 유체에서의 비선형 오일러 방정식(Nonlinear Euler's Equation)을 유도하는 글입니다.
몇달 전 다루었던 연속 방정식과 비슷한 내용으로, 오일러 방정식은 검사 체적 내 총 운동량의 변화와 유동 운동량의 관계를 정의하는 방정식입니다.
후술하겠지만, 유도된 오일러 방정식의 최종적인 형태를 보면 뉴턴의 운동 방정식(F = ma)과 같은 꼴이 나오게 됩니다.
이를 통해 오일러 방정식이 검사 체적에 작용하는 힘과 가속도, 검사 체적 내의 질량과의 관계를 규정한다고도 말할 수 있습니다.
오늘은 조금 내용이 복잡하여, 빠르게 시작하도록 하겠습니다.
연속 방정식을 유도할 때와 마찬가지로, 아래 그림과 같이 부피가 dV = dxdydz인 검사 체적의 각 축 방향대로 압력 P_x, P_y, P_z가 가해지는 상황을 가정하겠습니다.
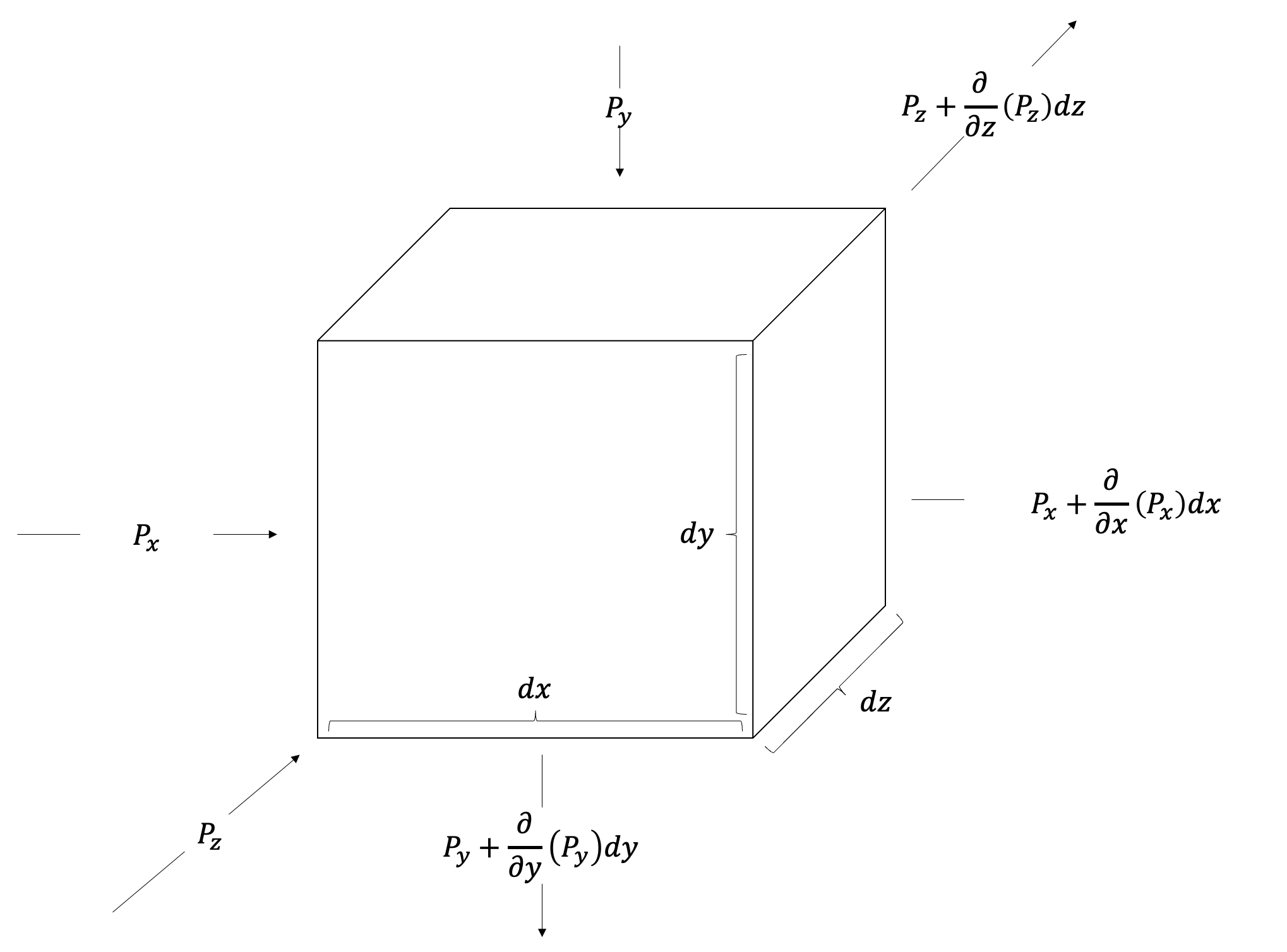
이 검사 체적의 x축, y축, z축의 방향으로 가해지는 알짜힘 f_x, f_y, f_z는 위 그림에서 양 방향으로 가해지는 압력 P와 그 증분 P+∂P/∂L dL의 차이입니다.
즉 두 힘을 빼 주면 된다는 것입니다.
연속 방정식과 비슷한 내용이니 아래에 간단히 유도 과정을 적어두겠습니다.

[Eq. 1~3]
검사 체적의 x, y, z축 방향 알짜힘은 각 축의 두 면으로 가해지는 압력의 크기의 차이이므로, 가해지는 두 압력을 빼 줍니다. 대괄호를 풀고 식을 간단하게 정리합니다.
결과적으로 검사 체적 dV의 내부에 가해지는 알짜 합력(Net force, df)는 각 방향 알짜힘을 모두 더한 것입니다.
3차원 델 연산자(3D Del Operator, Eq. 4)를 이용하여 식을 간단히 만들어 보겠습니다.

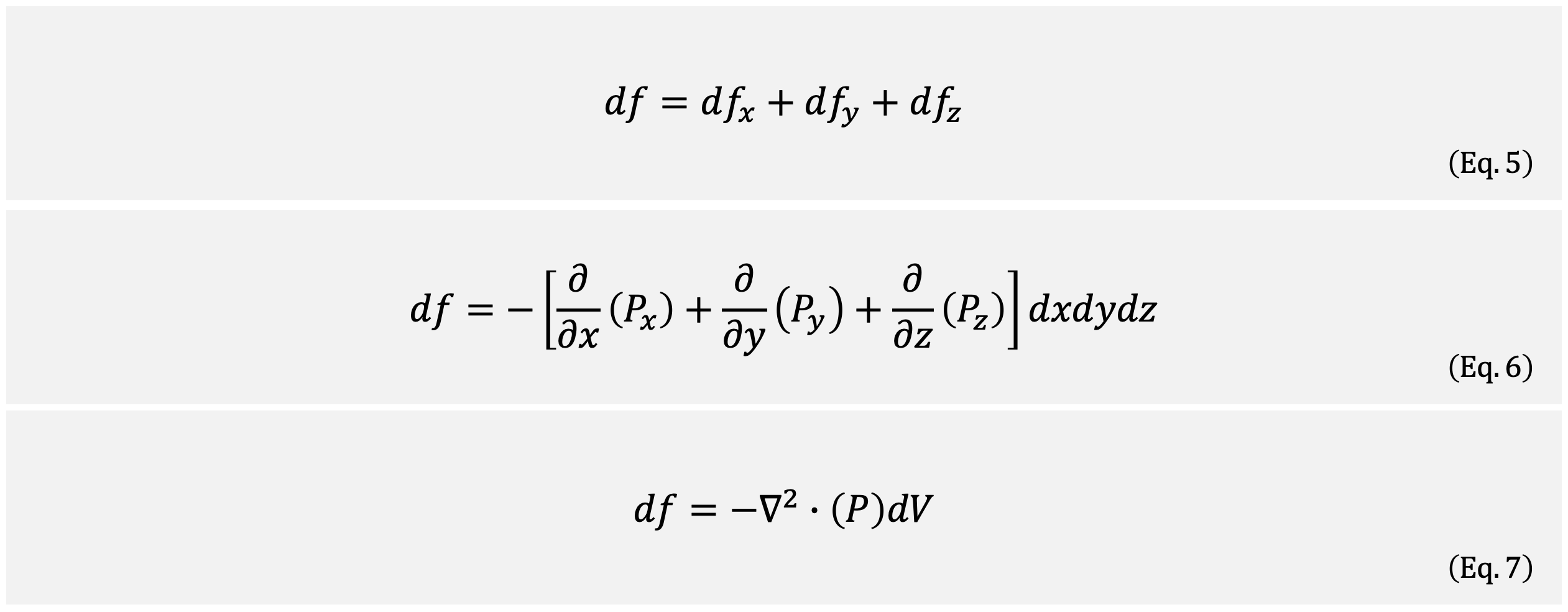
[Eq. 5]
검사 체적 dV에 가해지는 알짜 합력은 dx, dy, dz 성분 알짜 합력의 합입니다.
[Eq. 5 → Eq. 6]
Eqs. 1, 2, 3의 결과를 Eq. 5에 직접 대입합니다. 세 값이 모두 음수이므로, 음의 부호로 묶어 합해줍니다.
[Eq. 6 → Eq. 7]
3차원 델 연산자(3D Del Operator, Eq. 13)를 이용하여 Eq. 6의 대괄호 안의 항들을 간단하게 정리합니다.
Eq. 7의 알짜 합력은 검사 체적의 표면에 작용하는 표면력(Surface force)입니다.
그러나, 일반적으로 유체에는 표면력과 더불어 물체력(Physical force)도 같이 작용합니다. 물체력의 대표적인 예로는 중력이 있습니다.
따라서 dV에 작용하는 총 알짜힘(Total force)을 구하려면 알짜 합력(Eq. 7)에 중력항을 더해주어야 합니다.
간단한 조작을 통하여 알짜힘을 유도하겠습니다.

[Eq. 8]
검사 체적 dV에 가해지는 총 알짜힘은 알짜 합력(Eq. 7)과 중력항의 합입니다.
[Eq. 8 → Eq. 9]
Eq. 8의 우변의 첫 번째 항에는 Eq. 7을, 두 번째 항에는 중력항을 대입합니다. G = mg이고 m=ρdV임을 이용하여 중력항을 유도하였습니다.
Eq. 9에서 g는 중력 가속도로, 일반적인 크기는 g=9.8m/s^2입니다.
보다 자세히는 g=9.80665m/s^2라 되어있습니다.
일반적인 경우에서 중력과 같은 물체력은 음파의 전파에 많은 영향을 주진 않습니다만, 음파가 먼 거리를 전파할 때는 중력의 영향을 받으므로 반드시 물체력을 고려해 주어야 합니다.
Eq. 9는 dV에 작용하는 총 알짜힘을 의미합니다.
뉴턴의 운동 방정식인 F = ma에 의하여, Eq. 9는 검사 체적의 질량과 내부 가속도의 곱과 같습니다.
검사 체적의 내부에는 압축성 유동하는 비점성 유체가 가득 차있으므로, 검사 체적의 질량은 m=ρdV로 간단하게 구할 수 있습니다.
그러나, 가속도는 조금 복잡합니다.
검사 체적의 양쪽 두 경계에서의 입자 속도를 구한 후, 이를 수학적으로 조작해야 하기 때문입니다.
오늘 이 부분을 모두 다루기에는 글이 너무 길어지므로 가속도는 다음 시간에 구하도록 하겠습니다.

[Reference]
[1] L. E. Kinsler, A. R. Frey, A. B. Coppens, J. V. sanders, “Fundamentals of Acoustics” (in USA) John Wiley & Sons, Inc. (1999)
[2] D. T. Blackstock, "Fundamental of Physical Acoustics" (in USA), John Wiley & Sons Inc. (2000)
'Physical Acoustics :: 물리 음향학 > Linear Acoustics :: 선형 물리 음향학' 카테고리의 다른 글
| Linear Acoustics(선형 물리 음향학) :: 입자속도, 음향 임피던스 일반식 유도하기 (0) | 2024.03.09 |
|---|---|
| Linear Acoustics(선형 물리 음향학) :: 비선형 연속 방정식 (2) | 2023.02.16 |