Physical Acoustics(물리 음향학) :: 음파
안녕하세요, 효온민입니다!
드디어 오늘부터 물리 음향학 연재를 시작합니다.
그동안 올려드렸던 기초 물리학과 수학 포스트 연재는 이제 조금 줄어들고, 본격적으로 음향학 포스트 연재에 힘을 실어보려고 합니다.
그러나, 기초적인 이론 없이는 음향학을 이해하기 어려우므로 그동안 올려드렸던 물리학과 수학 포스트는 꼭 다시 복습해 주셨으면 좋겠습니다.
아무튼 이번 물리 음향학의 첫 글로는 '음파(Sonic Wave)'에 대한 내용을 다루어 보려고 합니다.
음파를 연구하는 학문인 음향학을 공부함에 있어 음파를 정확히, 정량적으로 정의하는 것은 정말로 중요하기 때문에 오늘 글도 꼭 집중해서 읽어주세요.
그럼 바로 시작하겠습니다.
'음파(Sonic Wave)'가 무엇일까요?
우리의 친절한 네이버는 음파를 "탄성체를 매질로 전파되는 파동"으로 정의합니다.
네, 끝났습니다.
음파의 정의는 사실 위의 문장으로 충분히 갈음하여 설명될 수 있습니다.
그러나 단순하게 위의 문장으로 음파를 설명하기에는 직관적이지도 않고, 또 명확하지도 않으며 이해하기도 쉽지 않습니다.
따라서 음파의 성질과 그 특성을 이용하여 아래와 같이 음파를 자세히, 그리고 쉽게 정의해 보도록 하겠습니다.
1. 소리는 음파의 범주에 속합니다.
특별한 문제가 있는 상황을 제외한 경우, 우리는 살아가면서 아주 많은 소리를 듣습니다.
우리가 듣는 소리, 그 무수히 많은 소리는 모두 '음파'입니다.
대기 중 공기의 분포가 비중있다는 전제 하에서, 우리가 듣는 소리는 공기 입자의 종방향 섭동을 통하여 전파되기 때문입니다.
공기 내 입자의 집합이 '압축'과 '팽창'하며 전파된다는 뜻입니다. (단일 입자의 압축과 팽창이 아닙니다. 입자 집합이 거동하는 모습을 비유적으로 표현한 것입니다.)
아래는 다분자 매질에서 음파가 전파될 때, 시간에 따른 매질 내 입자의 위치 변화를 간단하게 묘사한 그림입니다.

소리는 크기, 높낮이, 특색에 대한 세 가지의 기본적인 성질을 가집니다.
이를 각각 Amplitude(진폭), Frequency[Pitch](진동수, 음고), Timbre(음색)이라 합니다.
다들 아시다시피 Amplitude(진폭)를 나타내는 단위로는 Bel(벨), deciBel(데시벨), Pascal(파스칼), Bar(바) 등이 있습니다.
사실 벨(Bel, deciBel)류와 압력(Pa, Bar)류를 같은 부류로 싸잡아서 표현하기에는 조금 무리가 있습니다.
따라서 이거 관련해서는 나중에 다시 자세하게 다루겠습니다.
또한 Frequency(진동수)를 나타내는 단위로는 Hertz(헤르츠)가 있습니다. 단위 시간(1초) 동안 주기 운동의 반복 횟수를 나타냅니다.
마지막으로 Timbre(음색)을 나타내는 단위는, 없습니다.
네, 없습니다.
사실 없다기 보단 너무 많은 부분에 영향을 받아서 딱 명시적으로 집을 수가 없습니다. 다만, 대표적으로는 음파의 파형에 많은 영향을 받습니다.
2. 음파는 역학파입니다.
파동을 정의하는 것은 생략하겠습니다.
파동은 크게 역학파(Mechanical Wave)와 전자기파(Electromagnetic Wave)로 나뉩니다. 파동의 전파가 매질의 유무에 영향을 받는지 그 여부에 의하여 나뉘는 것입니다.
음파는 역학파이며, 반드시 매질이 있어야 전파될 수 있습니다.
또한 음파의 전파 특성은 매질에 따라 달라집니다. 대표적으로 음속(Sound[Sonic] Speed)이 있습니다.
나중에 다시 자세하게 다루겠지만, 음속은 매질에 인가된 압력과 밀도와 온도의 함수입니다.
선형 음향학에서는 압력에 따른 음속의 변화가 작으므로 압력을 변수에서 제외하고 보면, 매질의 밀도가 높을 수록, 또 매질의 온도가 높을 수록 매질 내 음속이 빨라집니다.
따라서 아래와 같이 매질의 단열 체적 팽창 계수(Adiabat Bulk Modulus) B와 매질 내 평형 밀도 ρ_0의 비로 음속이 정의됩니다.
주제에서 조금 벗어나는 내용이므로 이 글에서는 B를 직접 유도하지는 않았습니다. 나중에 다시 자세하게 다루겠지만, 단열 체적 팽창 계수 B는 압력을 밀도로 미분한 값에 평형 밀도를 곱한 값입니다.

[Eq. 1]
선형 음향학에서, 단열 체적 팽창 계수 B와 평형 밀도의 비는 제곱된 음속을 나타냅니다. B를 직접 대입하여 평형 밀도 ρ_0를 약분하면, 편도함수만 남습니다.
[Eq. 2]
즉, 선형 음향학에서 압력을 밀도로 미분한 값은 제곱된 음속의 정의입니다.
또한 매질에 따라서 음파의 손실 정도나 선형성의 여부가 결정됩니다.
나중에 다시 다룰 예정인 선형 동차 유손실(점성력) 음향 파동 방정식(Linear Homogeneous Loss Acoustic Wave Equation)과 비선형 비동차 유손실 음향 파동 방정식(Nonlinear Inhomogeneous Loss Acoustic Wave Equation)을 아래에 써놓겠습니다. 아래 두 식을 통해 점성력에 의한 손실이 고려된 음파의 음압 분포와, 비선형파의 음압 분포를 예측할 수 있습니다.

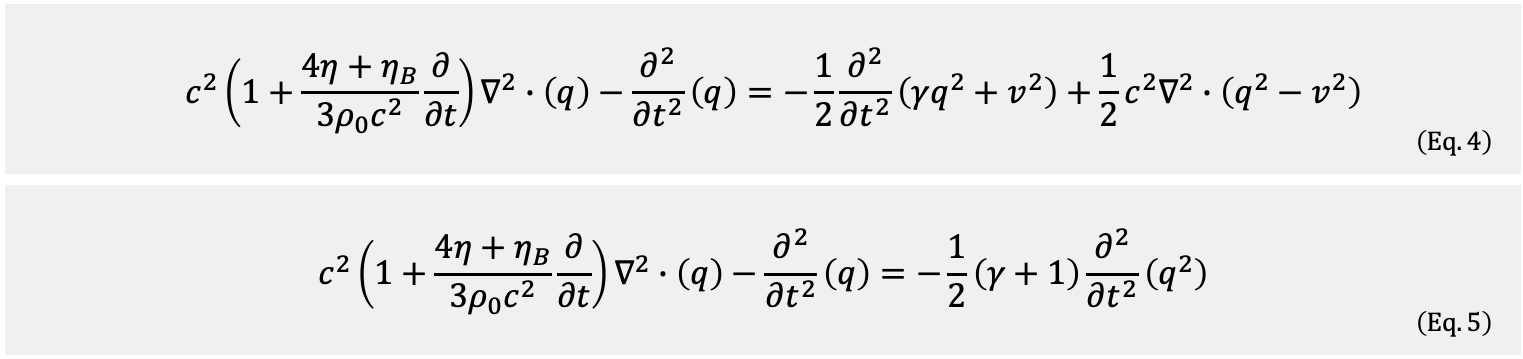
[Eq. 4 → Eq. 5]
Eq. 4의 우변에서 비선형성이 약한 항들을 제외시키면, 식을 Eq. 5와 같이 단순화시킬 수 있습니다. 나중에 다시 소개해드리겠습니다.
즉 매질은 음파의 전파에 아주 큰 영향을 미치므로, 정말로 중요한 음향학적 요소입니다.
오늘 내용은 여기까지입니다.
처음 올리는 음향학 글인 만큼 쉽고 재미있게 설명드리고 싶었는데, 마음처럼 되질 않습니다.
복잡하고 어려운 음향학 이론을 쉽게 설명할 수 있는 수준이 될 때까지 꾸준히 공부해 보겠습니다.
궁금하신 점 있으면 언제든지 댓글로 남겨주세요!
확인 후 답변드리겠습니다.
감사합니다.
2023. 02. 15
효온민 올림
[Reference]
[1] Lawrence E. Kinsler, “Fundamentals of Acoustics” (in USA), John Wily & Sons Inc. (1999)
[2] S.W. Rienstra, "An Introduction to Acoustics" (in Netherlands), Eindhoven University of Technology. (2021)
Copyrights ⓒ Hyonmin.